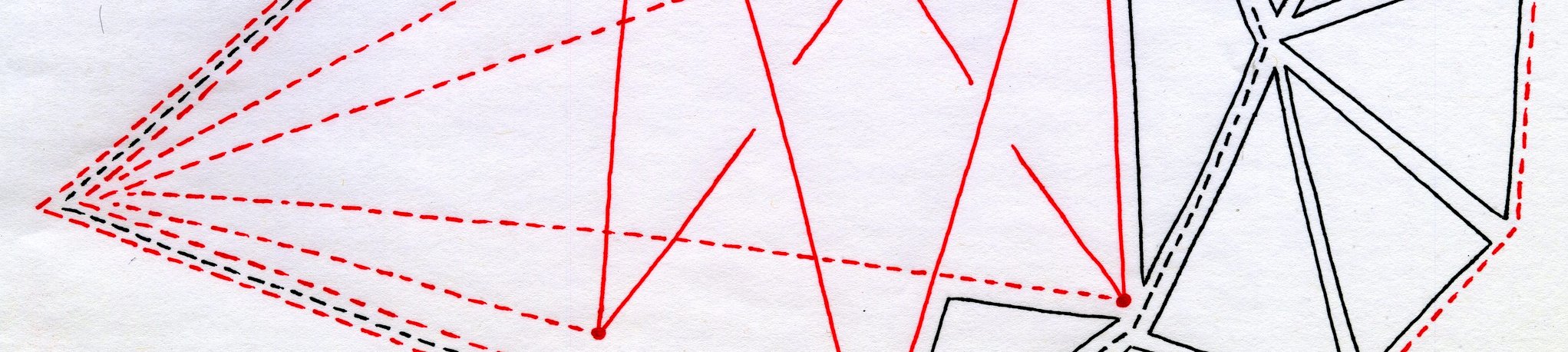
-
D32. Tangellipses
Posted: 2025 Dec 24 Solutions will be accepted through 2025 Jan 2We’ve featured a few Dilemmas from PMP participants about the properties of ellipses. But it turns out that they are a perennial source of interesting questions and problems for the entire mathematical community. For example, six years ago, when the Problem Warden was the Playground editor for the Mathematical Association of America, he wrote down…
-
D31. Mono Nonograms
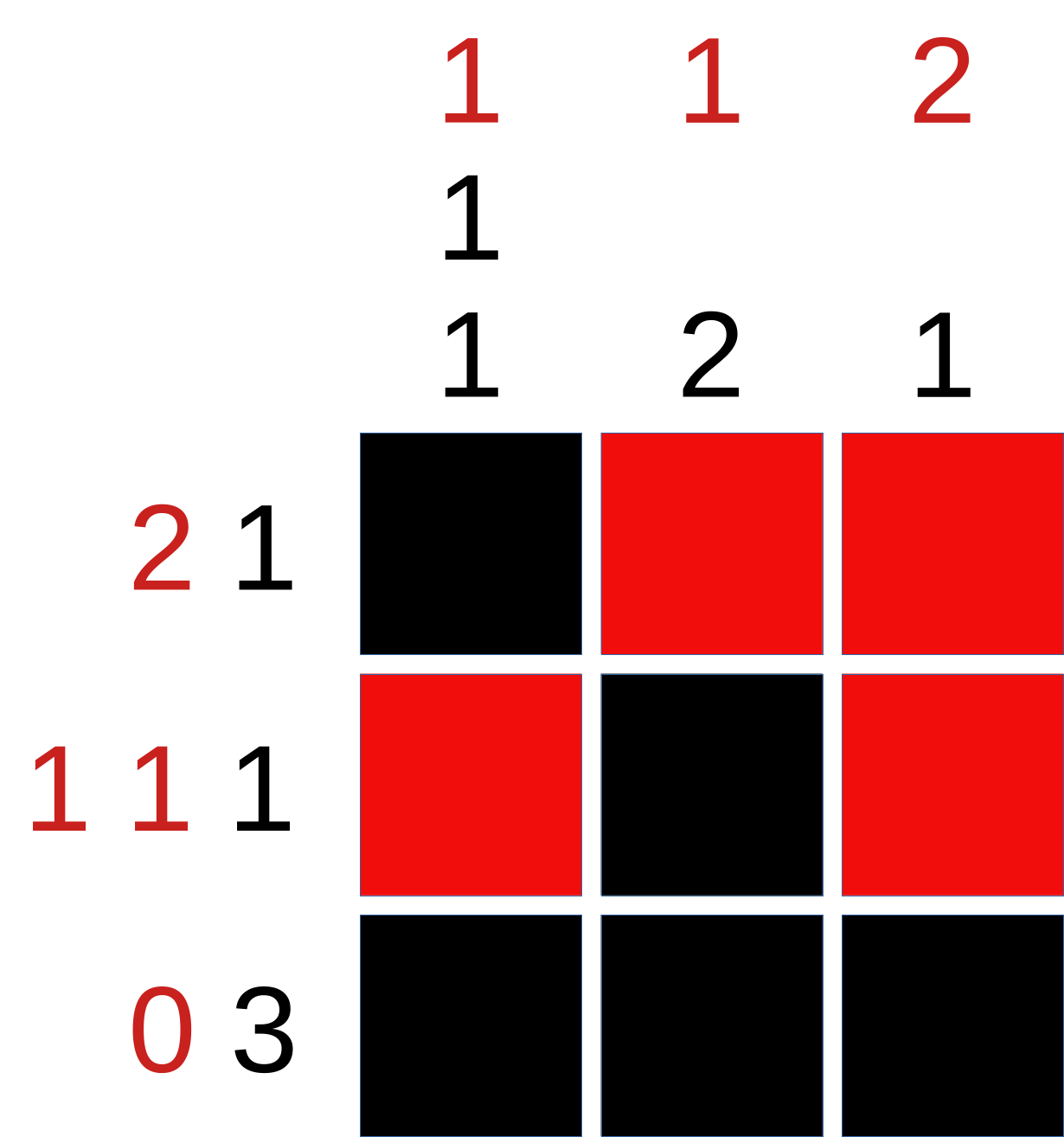Posted: 2025 Dec 24 Solutions will be accepted through 2025 Jan 2These problems are based on a type of puzzle called a nonogram: you are given a grid (usually a rectangular portion of a square grid), and each row and column is labeled with a list of numbers that gives the sizes of the blocks of consecutive squares that should be colored black in that row…
-
D30. Disambiguated Triangle
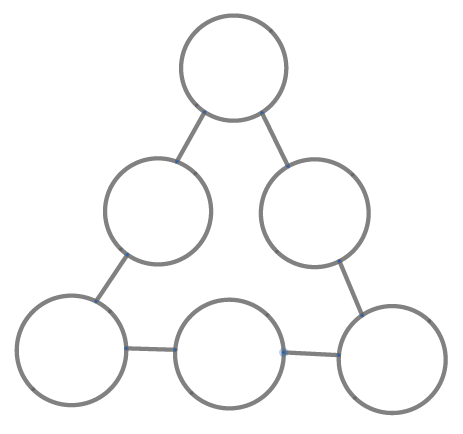Posted: 2025 Dec 24 Solutions will be accepted through 2025 Jan 2These questions are based on a puzzle that new contributor Stanley Wu-Wei Liu picked up from WeChat and translated from Chinese for us. Your friend tells you that they have placed the six numbers 2, 3, 4, 5, 6, and 7 in the circles in the diagram in the figure to the left so that…
-
D29. Geometric-Trigonometric Inequality
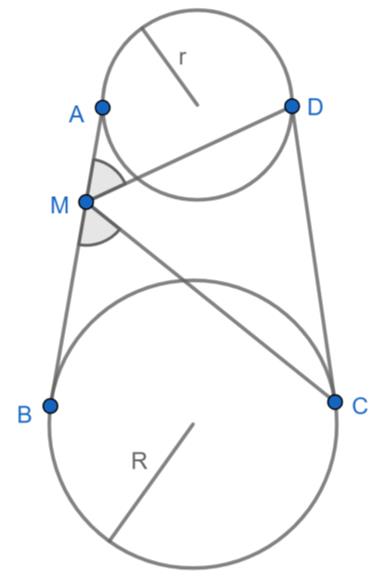Posted: 2025 Dec 23 Solutions will be accepted through 2025 Jan 2Since no respondents provided a solution to his last problem, Prof. Aliyev is willing to offer one more chance to unravel his mysterious diagrams. In the accompanying figure, nonintersecting circles with radii r < R have common external tangent lines A B and C D , where the named points are the points of tangency.…
-
D28. Tile Troubles
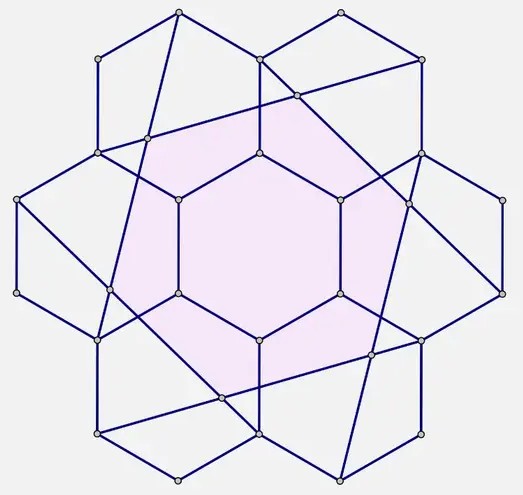Posted: 2025 May 12 Solutions will be accepted through 2025 Jul 15Dr. Arsalan Wares’ letter this month is beautiful, as always, but sadly recounts a tale of honeycomb horror. The diagram in Figure 3 depicts a portion of a tiling of the plane by regular hexagonal tiles. All line segments shown have endpoints at the vertices of the tiling. Dr. Wares woke up one morning to…
-
D27. Penned Out
Posted: 2025 May 12 Solutions will be accepted through 2025 Jul 15Figure 1 (below left) shows a perfect two-point perspective diagram of Farmer Nell’s red-roofed barn and precisely square pigpen in front of it. (“Two-point perspective” means that all lines that are vertical in three dimensions appear perfectly vertical in the diagram, while any two parallel horizontal lines intersect on the horizon line N E .)…
-
D26. Aperiodic Partition
Posted: 2025 May 12 Solutions will be accepted through 2025 Jul 15(with thanks to Kate Stange, University of Colorado) Recall that an (infinite) arithmetic progression is the set of all numbers of the form a + n d , where a and d are fixed and n is any natural number. For example, 5, 8, 11, 14, … , and so on forever, is an arithmetic…
-
D25. Whodunni’s Shuffle
Posted: 2025 May 12 Solutions will be accepted through 2025 Jul 15Our frequent contributor Prof. Stewart is back with a bit of permutation prestidigitation: The great stage magician Harry Whodunni shuffles a pack of (more than two) cards in the following simple way: he moves the top card to the next-to-bottom position, and then turns the whole pack over (which has the side effect of turning…
-
D24. Sliding Ratios
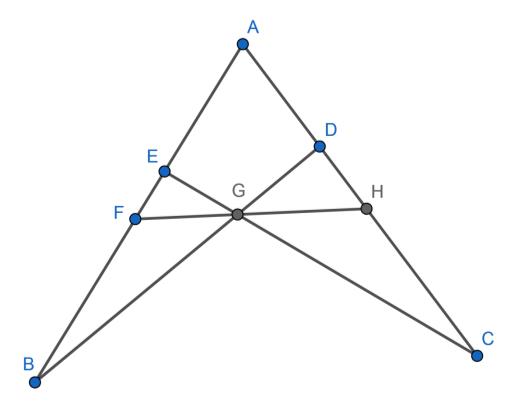Posted: 2024 Sep 30 Solutions will be accepted through 2025 Jul 15As shown in Figure 4, A B C is a triangle. Points F and E lie on side A B , with F closer to B . Point D lies on side A C . Point G is the intersection of segments B D and C E , and H is the intersection of ray…
-
D23. Factor Network
Posted: 2024 Sep 30You want to label the vertices (corners) of a regular octahedron (see Figure 3) with whole numbers bigger than one so that the labels of two vertices have a common factor (bigger than one) if and only if they are adjacent on the octahedron (connected by an edge). Is it possible? If so, what is…