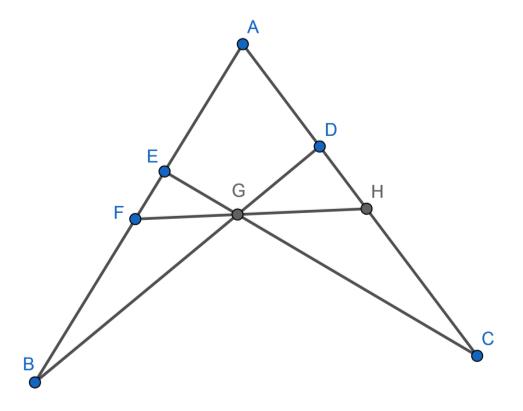
Sliding Ratios – The Prisoner's Dilemma

Figure 4: Pivoting segment $F H$ about $G$ to cut $B E$ and $C D$ into two pieces each.

As shown in Figure 4, $A B C$ is a triangle. Points $F$ and $E$ lie on side $A B$ , with $F$ closer to $B$ . Point $D$ lies on side $A C$ . Point $G$ is the intersection of segments $B D$ and $C E$ , and $H$ is the intersection of ray $F G$ with side $A C$ . Prove that it must always be the case in this situation that

$\frac{B F}{F E} > \frac{D H}{H C},$

where in this inequality, $B F$ (for example) denotes the length of the corresponding segment.

D24. Sliding Ratios