-
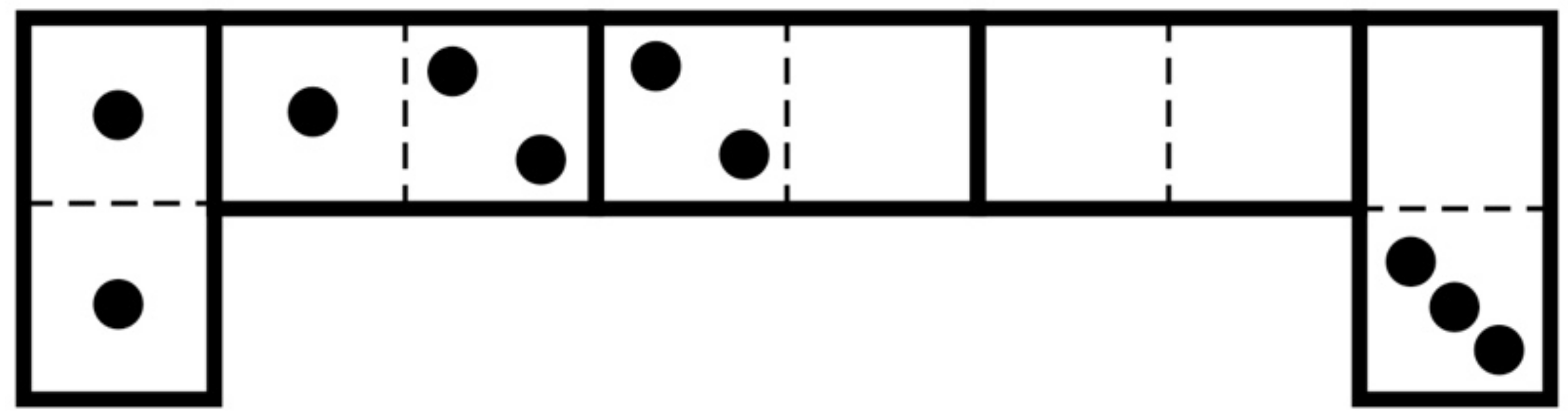
D18. Domino Design
 Posted: 2024 Mar 01
Posted: 2024 Mar 01In the arrangement of five dominoes shown in Figure 1, obeying the usual rule that adjacent squares have matching numbers, the two at the end total five spots, and so do the three in the middle. There are three other ways to achieve this, not counting left-right reflections as different. Can you find them?
-
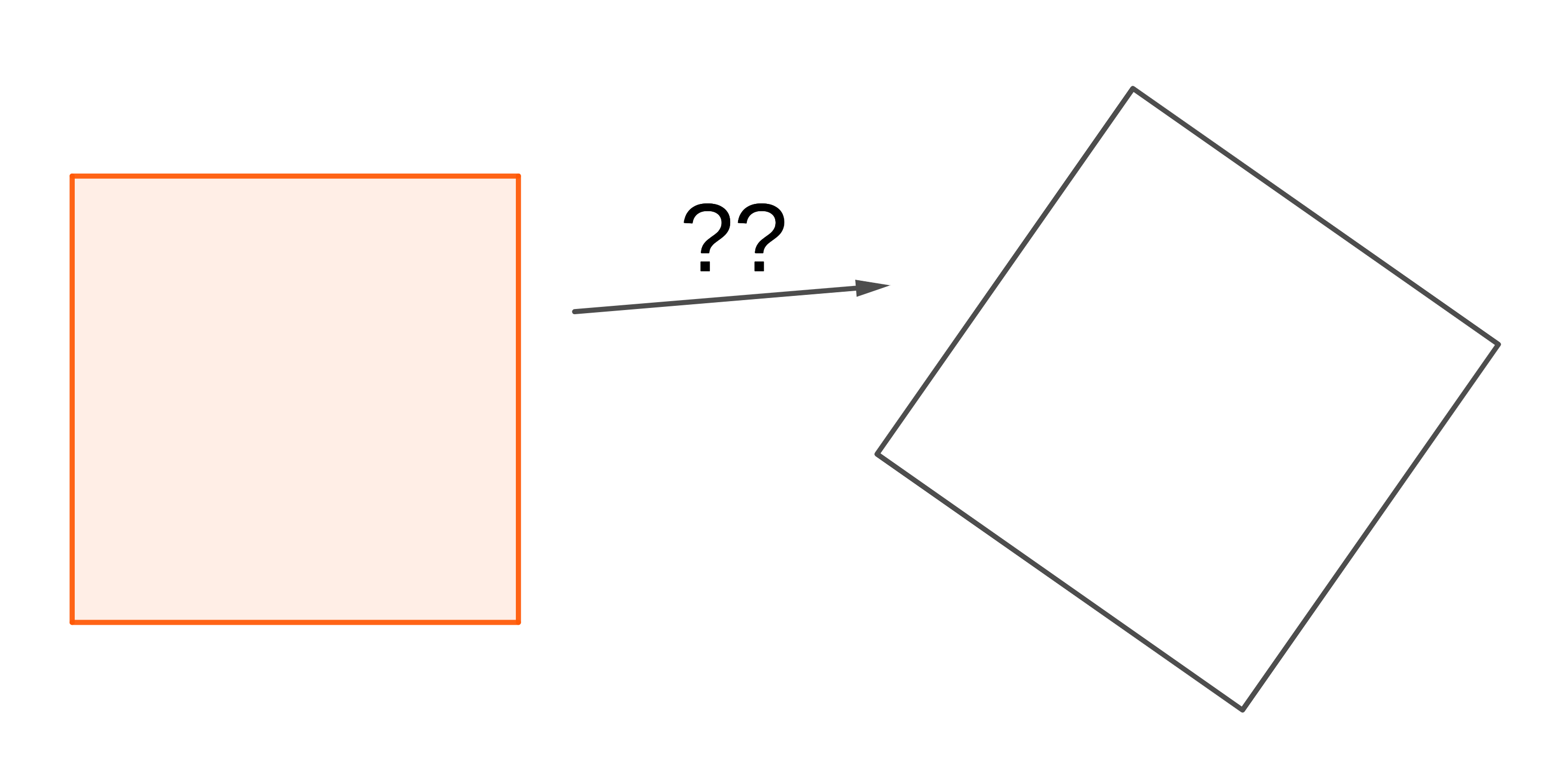
D17. Transrotation
 Posted: 2023 Nov 15
Posted: 2023 Nov 15Often you can slice up one shape and reassemble the pieces to make a different shape, like the famous square-to-triangle dissection shown in Figure 1. Notice that in this rearrangement you are forced to rotate some of the pieces when you put them back together. Sometimes, though, you can do the assembly by only translating…
-
D16. Five Choices
 Posted: 2023 Nov 15
Posted: 2023 Nov 15You are at a crossroads with five roads leading away from it, and you don’t know which direction to go. You would like to choose randomly, with equal probability for each road. If your only way of making random choices is to flip a fair coin (one that could come up heads or tails with…
-
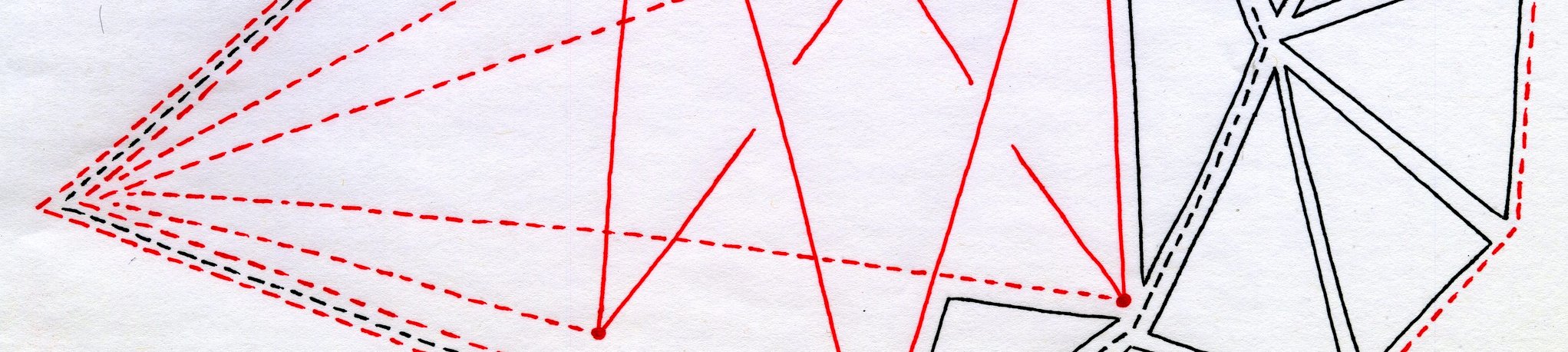
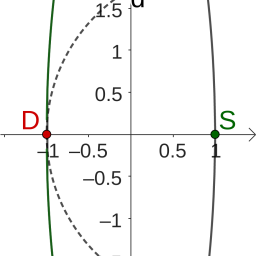
D15. Eccentric Repulsion
 Posted: 2023 Nov 15
Posted: 2023 Nov 15Paul is back with another elliptical quandary. Suppose you are constrained to a circular track, which we will model as the unit circle in the plane, and there is something smelly at one point on the track, say where it intersects the x -axis at the point ( 1 , 0 ) . If you…
-
D14. Flip Functions
 Posted: 2023 Nov 15
Posted: 2023 Nov 15Call a function f mapping the real numbers to themselves a sign-flipping function if for all x , y ∈ R , ( x − y ) ( f ( x ) + f ( y ) ) = ( x + y ) f ( x − y ) . For example, the identity…
-
D13. The Experbola
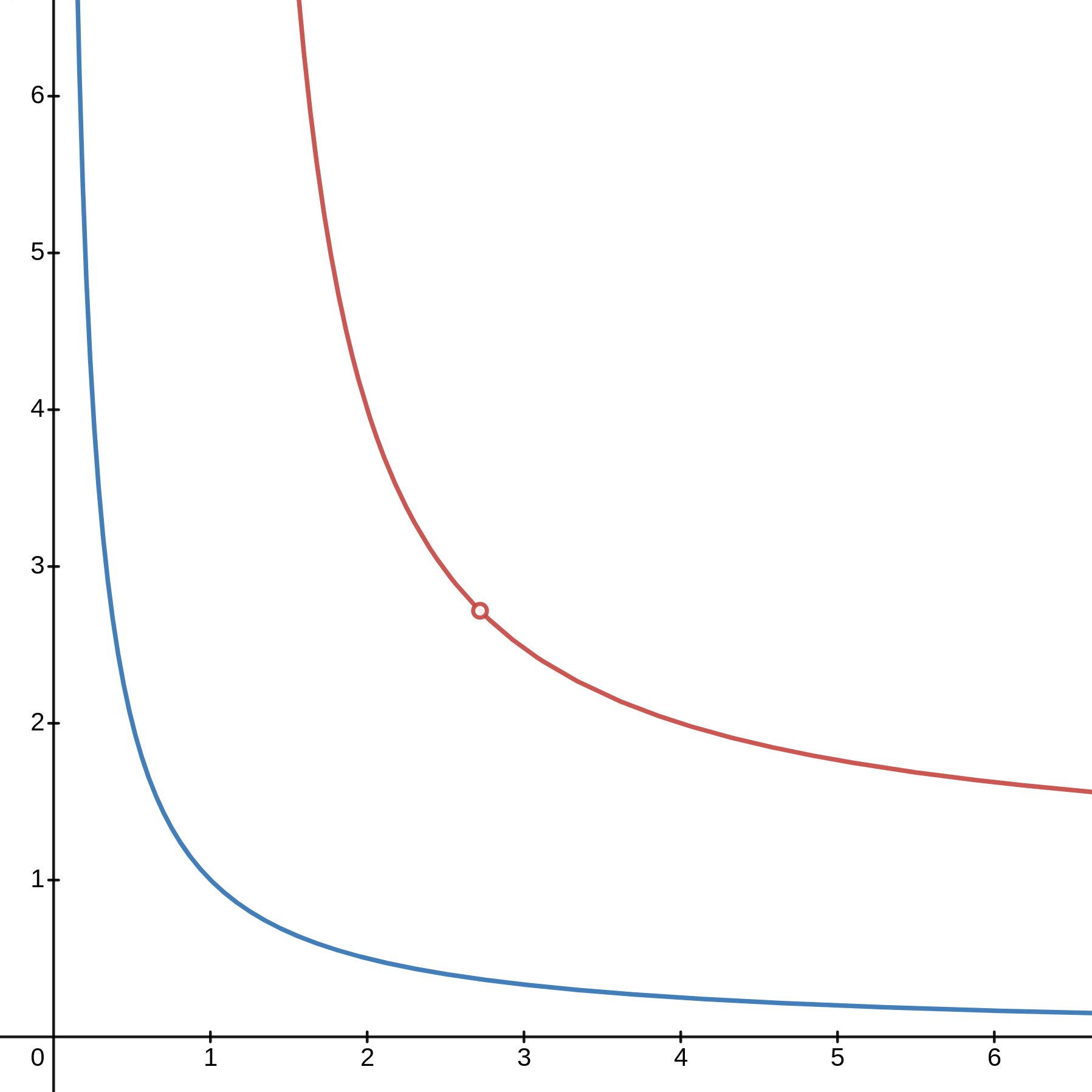 Posted: 2023 May 01
Posted: 2023 May 01In Dilemma 8, we investigated a curve similar to an ellipse, but changing addition to multiplication in its definition. This time, PMP participant William Keehn proposes a similar exploration related to the hyperbola, another conic section, which can be thought of as all of the points ( x , y ) in the plane where…
-
D12. Strange Coincidence
 Posted: 2023 May 01
Posted: 2023 May 01Let’s listen in on a conversation between siblings divided by math, so to speak: “That’s amazing!” said Mathophila. “The squares of three consecutive positive whole numbers add up to the same number as the squares of the next two numbers.” “Oh, no big deal, that must happen all the time,” replied her brother, Innumeratus. “I…
-
D11. Octosection
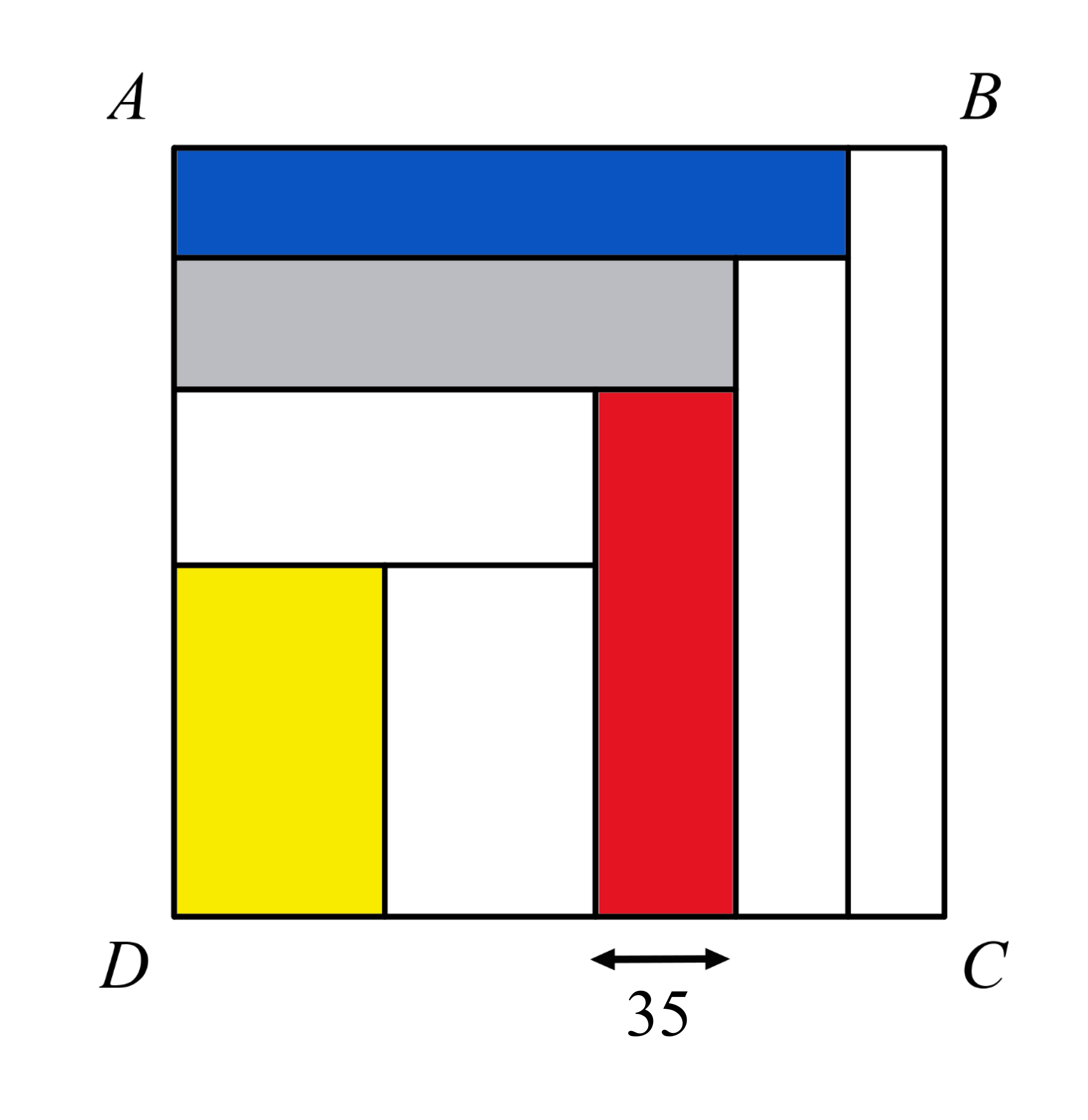 Posted: 2023 May 01
Posted: 2023 May 01Square A B C D in Figure 1 has been dissected into eight equal-area rectangles. The width of the rectangle shaded red in Figure 1 is 35 units. What is the area of square A B C D ? For a bonus challenge, can you devise and solve a similar problem that dissects a square…
-
D10. Half-and-half Hanoi
 Posted: 2023 May 01
Posted: 2023 May 01You may be familiar with the Tower of Hanoi puzzle in which you start with eight discs stacked on one of three pegs, each disc smaller than the one below it. The other two pegs are empty. The goal of the puzzle is to move the entire stack of discs to a different peg, according…
-
D9. Semi Inellipse
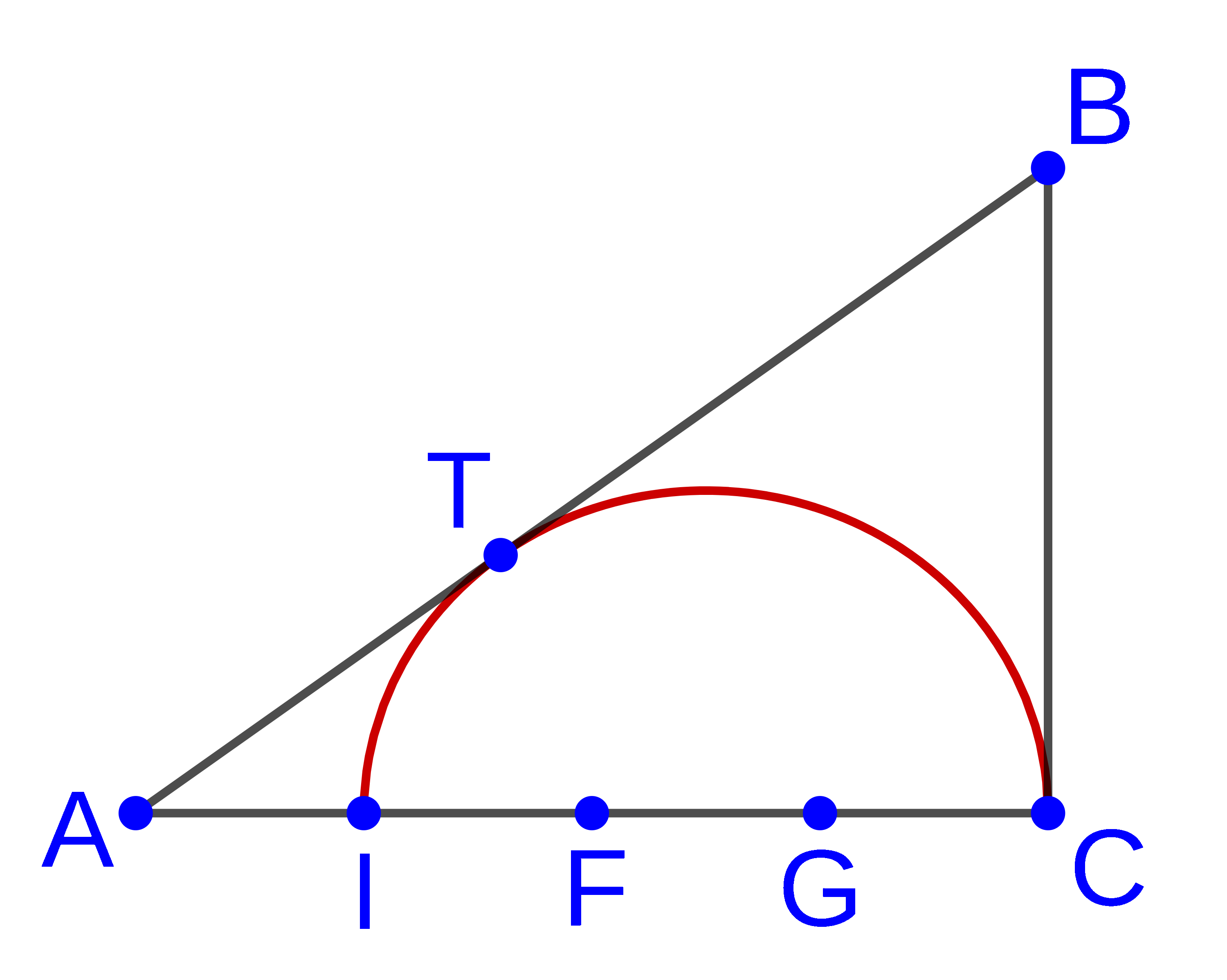 Posted: 2022 Sep 15
Posted: 2022 Sep 15PMP participant Paul Morton has also investigated the properties of ellipses. As shown in Figure 1, semiellipse C T I is inscribed in right triangle C B A so that it is tangent to hypotenuse A B at T , and so that points I and the two foci F and G of the ellipse…