The Prisoner's Dilemma

In Dilemma 8, we investigated a curve similar to an ellipse, but changing addition to multiplication in its definition. This time, PMP participant William Keehn proposes a similar exploration related to the hyperbola, another conic section, which can be thought of as all of the points $(x,y)$ in the plane where $xy=1.$ Since that description already involves multiplication, this time we will move on to exponentiation.

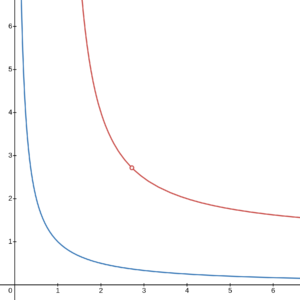
So, now consider all of the points where $x^y=y^x$ such that $x$ and $y$ are distinct positive real numbers. You get a curve somewhat resembling a hyperbola, that William has dubbed the “experbola.” Figure 1 shows the hyperbola and experbola side-by-side. And William is brimming with interesting questions about the experbola, so Dilemma 13 has lots of parts:

1. Find all of the points on the experbola where both coordinates are whole numbers. (And explain why there aren’t any others.)
2. An asymptote of a curve is a straight line that the curve becomes arbitrarily close to but never touches. For example, the hyperbola in Figure 1 has two asymptotes: the lines $x=0$ and $y=0.$ Does the experbola have any asymptotes? If so, find them.
3. The condition that $x$ and $y$ are distinct is needed because whenever they are the same, the equation $x^y=y^x$ is trivially satisfied. So without that condition, the experbola would include the entire diagonal line $x=y.$ But as you can see in Figure 1, that condition also cuts the experbola into two disconnected pieces. However, there is a unique single point on the line $x=y$ that you could add back to the experbola to “complete” it and make it a single continuous curve. (That’s the point indicated by the small red open circle in Figure 1.) What are the coordinates of that point?
4. Find (continuous, non-constant) functions $f(t)$ and $g(t)$ such that the point $(f(t),g(t))$ is on the experbola for all positive real numbers $t$. For this one, William offers a hint, by way of an example: $(\sqrt{3}{)}^{3\sqrt{3}}=(3\sqrt{3}{)}^{\sqrt{3}}.$ Such a pair of functions is called a parametrization of the experbola, or at least of the part of the experbola it lands on.