-
D24. Sliding Ratios
 Posted: 2024 Sep 30 Solutions will be accepted through 2024 Dec 31
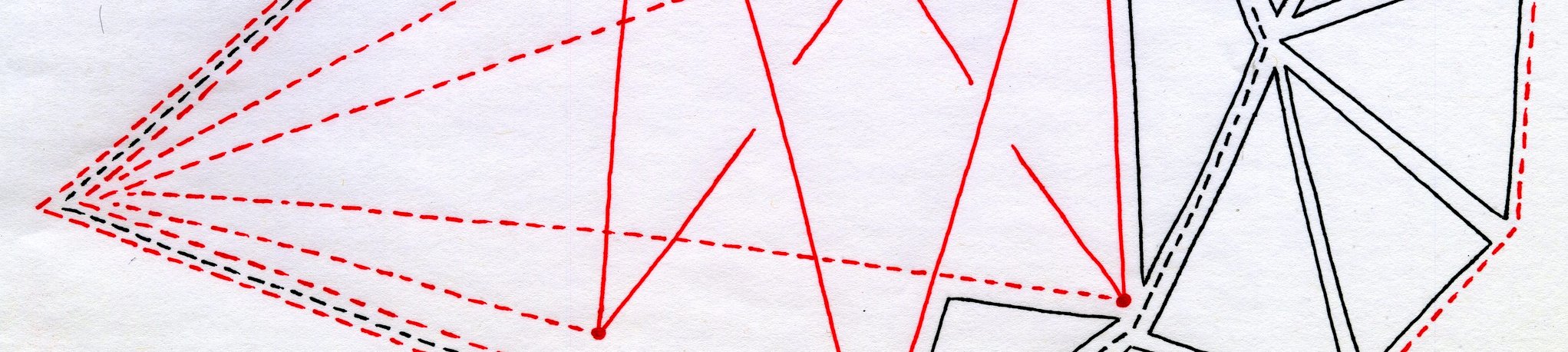
Posted: 2024 Sep 30 Solutions will be accepted through 2024 Dec 31Prof. Aliyev is back, this time with a geometry problem. As shown in Figure 4, A B C is a triangle. Points F and E lie on side AB, with F closer to B . Point D lies on side A C . Point G is the intersection of segments B D and C E…
-
D23. Factor Network
Posted: 2024 Sep 30 Solutions will be accepted through 2024 Dec 31You want to label the vertices (corners) of a regular octahedron (see Figure 3) with whole numbers bigger than one so that the labels of two vertices have a common factor (bigger than one) if and only if they are adjacent on the octahedron (connected by an edge). Is it possible? If so, what is…
-
D22. Fill the Jar
 Posted: 2024 Sep 10 Solutions will be accepted through 2024 Dec 31
Posted: 2024 Sep 10 Solutions will be accepted through 2024 Dec 31You are making sugar cookies from a batch of dough in the following way: You take your dough and roll it into a perfect square of just the right thickness (you are a very precise baker). Then you cut out 1-inch radius, perfectly circular, cookies arranged in a square grid so that the cookies are…
-
D21. Light Chase
 Posted: 2024 Sep 10 Solutions will be accepted through 2024 Dec 31
Posted: 2024 Sep 10 Solutions will be accepted through 2024 Dec 31You have a puzzle toy which consists of a ring of lit buttons, each of which can glow red, yellow, or (bluish-)green, as illustrated in Figure 1. When you push a button, its color cycles in the order red → green → yellow → red. The catch is, the lights two positions away in each…
-
D20. Geometry Game
 Posted: 2024 Mar 01
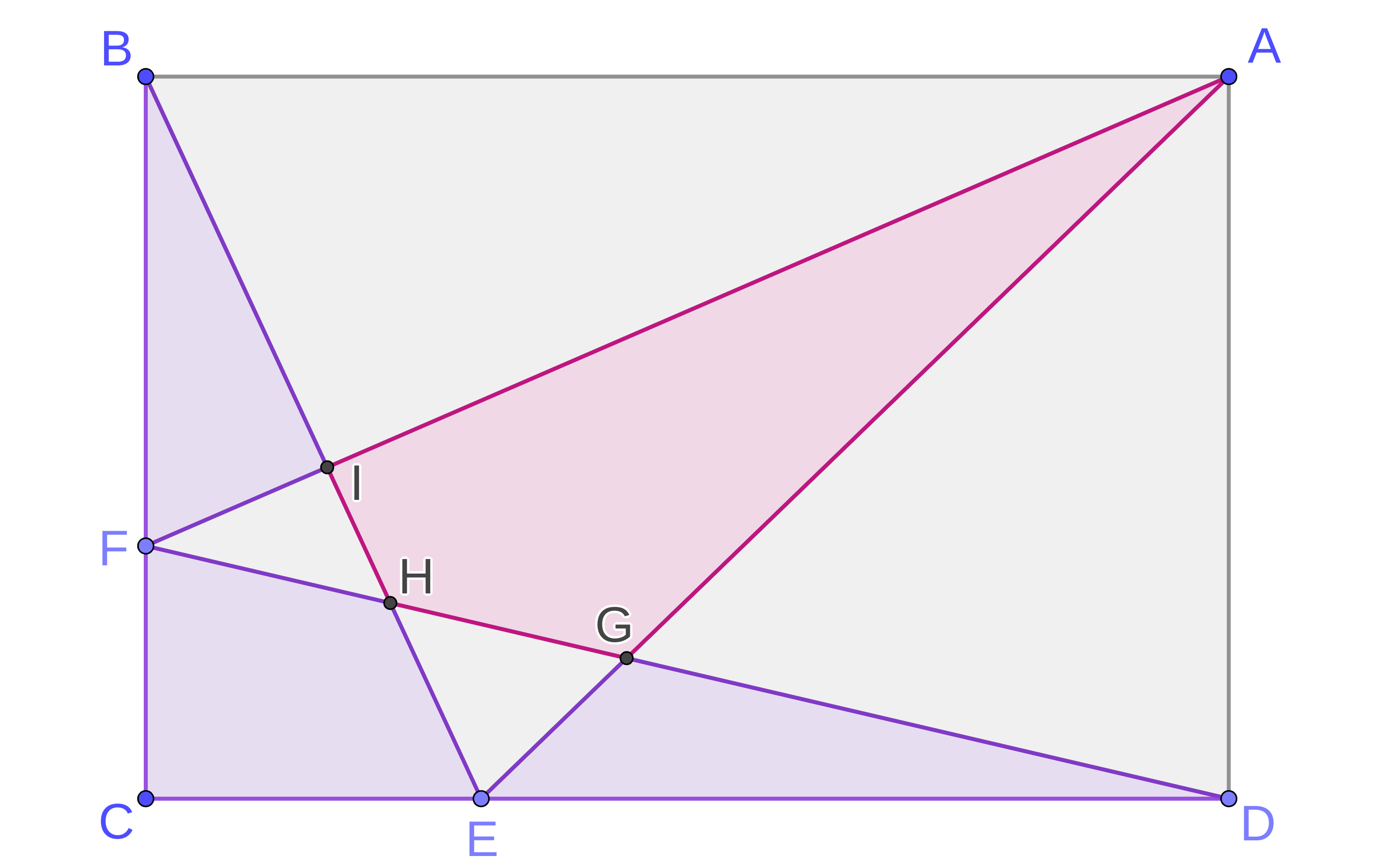
Posted: 2024 Mar 01You and a buddy start with a rectangular cake, represented by rectangle A B C D in Figure 1. Then you get to pick any point E between C and D , and the cake is sliced with two straight cuts, from B to E and E to A . Then it’s your friend’s turn…
-
D19. Covid Conundrum
 Posted: 2024 Mar 01
Posted: 2024 Mar 01Suppose you stood on line as part of a group of 30 people waiting to receive a vaccine. After everyone finished, you were told that ten members of the group turned out to have cases of Covid. You never came down with the infection, so you couldn’t have been one of the ten. If you…
-
D18. Domino Design
 Posted: 2024 Mar 01
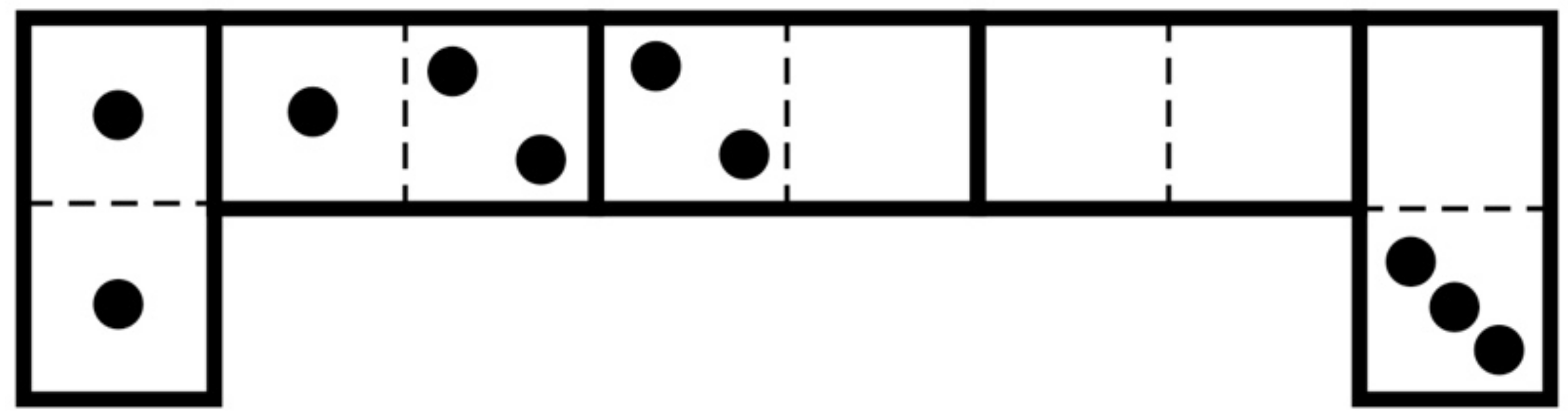
Posted: 2024 Mar 01In the arrangement of five dominoes shown in Figure 1, obeying the usual rule that adjacent squares have matching numbers, the two at the end total five spots, and so do the three in the middle. There are three other ways to achieve this, not counting left-right reflections as different. Can you find them?
-
D17. Transrotation
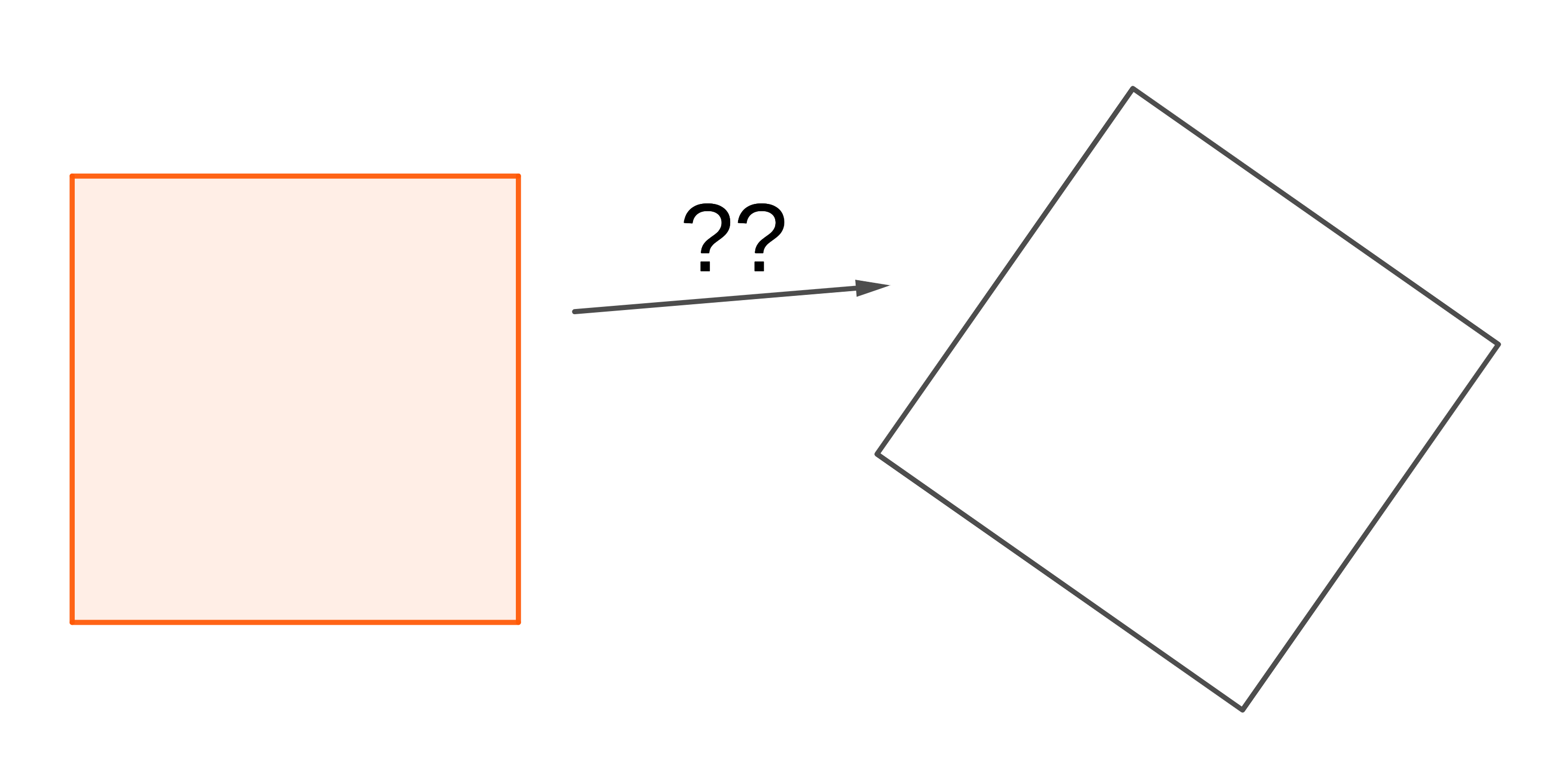 Posted: 2023 Nov 15 Solutions will be accepted through 2024 Dec 31
Posted: 2023 Nov 15 Solutions will be accepted through 2024 Dec 31Often you can slice up one shape and reassemble the pieces to make a different shape, like the famous square-to-triangle dissection shown in Figure 1. Notice that in this rearrangement you are forced to rotate some of the pieces when you put them back together. Sometimes, though, you can do the assembly by only translating…
-
D16. Five Choices
 Posted: 2023 Nov 15
Posted: 2023 Nov 15You are at a crossroads with five roads leading away from it, and you don’t know which direction to go. You would like to choose randomly, with equal probability for each road. If your only way of making random choices is to flip a fair coin (one that could come up heads or tails with…
-
D15. Eccentric Repulsion
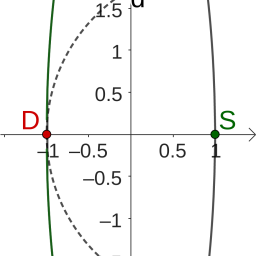 Posted: 2023 Nov 15
Posted: 2023 Nov 15Paul is back with another elliptical quandary. Suppose you are constrained to a circular track, which we will model as the unit circle in the plane, and there is something smelly at one point on the track, say where it intersects the x -axis at the point ( 1 , 0 ) . If you…