Contributed by Ian Stewart, University of Warwick.
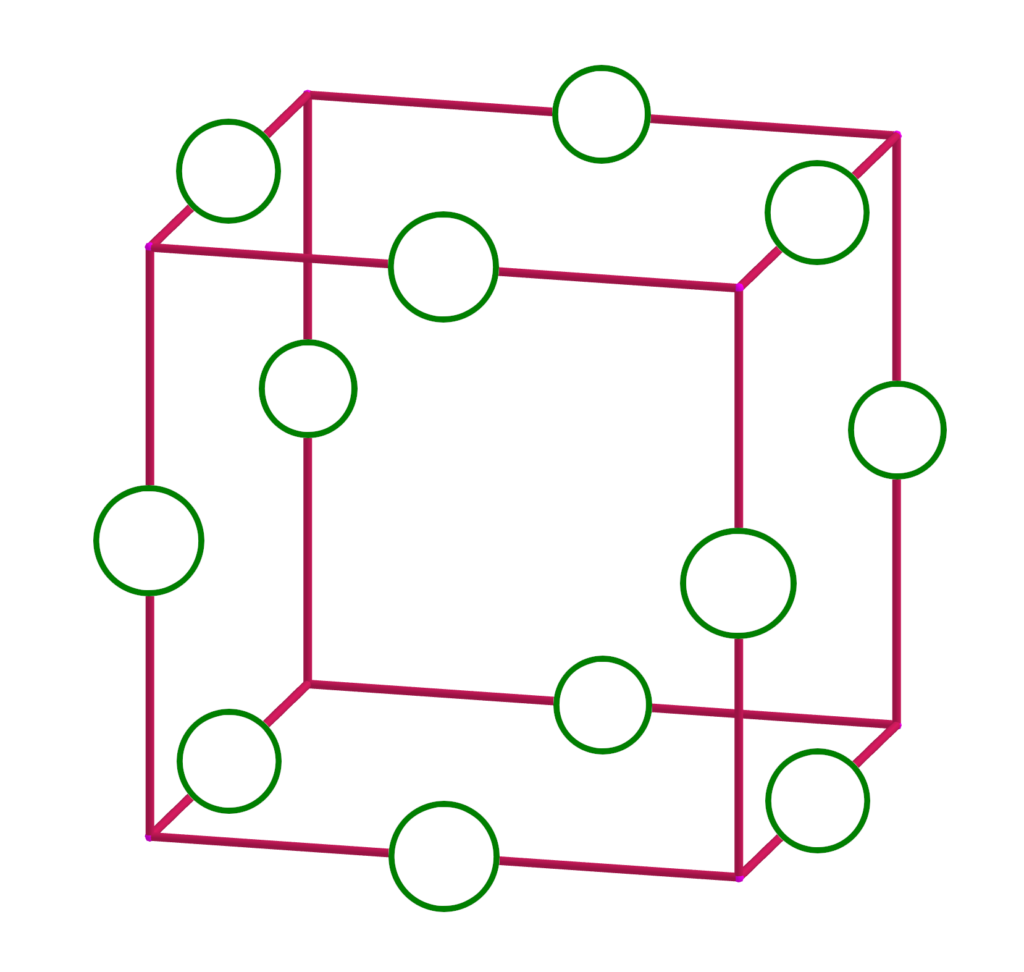
Is it possible to number the edges of a cube using each of the numbers -6, -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, and 6 once, so that for every vertex, the sum of the numbers on the edges that meet there is zero? What about if instead you use the 12 consecutive integers from -5 to 6, inclusive?
This problem originally appeared in The Prisoner’s Dilemma in the 2022 Winter issue of the PMP Newsletter. Solutions will be accepted through 2022 May 27.