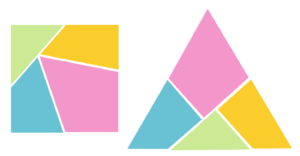
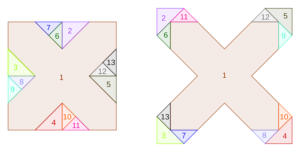
Often you can slice up one shape and reassemble the pieces to make a different shape, like the famous square-to-triangle dissection shown in Figure 1. Notice that in this rearrangement you are forced to rotate some of the pieces when you put them back together. Sometimes, though, you can do the assembly by only translating the pieces, i.e. sliding them without rotation, as in the square-to-cross dissection shown in Figure 2.
But is it possible to start with a square and “rotate by translation?” In other words, can you dissect a square into finitely many pieces, and translate each of them without any rotation, to reassemble them into the shape of a square that has been rotated (by some angle other than a multiple of )? This goal is schematically shown in Figure 3. Note that although this problem was suggested to the Prisoner’s Dilemma by Akiva, it was apparently first posed by Hugo Hadwiger way back in 1950.