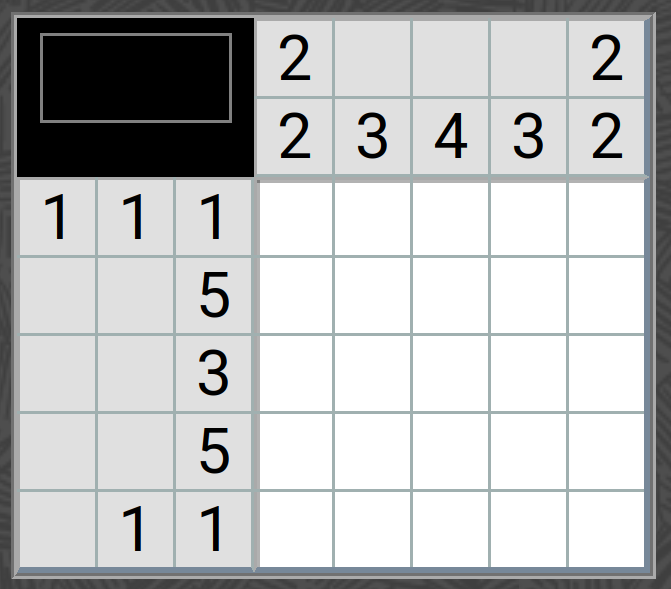
These problems are based on a type of puzzle called a nonogram: you are given a grid (usually a rectangular portion of a square grid), and each row and column is labeled with a list of numbers that gives the sizes of the blocks of consecutive squares that should be colored black in that row or column. (Each block of black squares must be separated by one or more unfilled squares.)
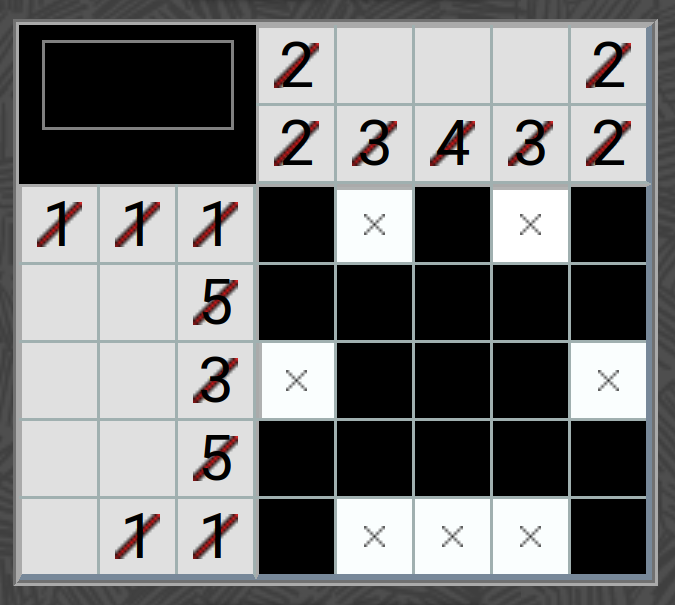
For example, you might have clues as on the leftmost figure below (with thanks to onlinenonograms.com), which you can figure out must be filled in as on its right.
- You may notice, however, that some clues have been used more than once in this puzzle: two different rows have the clue “5,” two columns and a row have the clue “3,” and two columns have clue “2 2.” What is the smallest possible rectangular square-grid nonogram in which every clue is different? Note that you must not even use the same clue for both a row and a column.
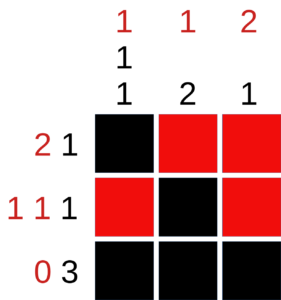
- For an even more brain-bending challenge, consider a variation in which every cell must be colored either red or black (no square can be left unfilled) and you get both the “red clue” and the “black clue” for each row and column. The final figure below shows a tiny solved red-black nonogram. Can you find an 8×8 red-black nonogram in which all of the black clues are different, and all of the red clues are different? (There will have to be some overlap between the black clues and the red clues — do you see why?)